MATH 4275/6275 Applied Dynamical Systems [Syllabus]

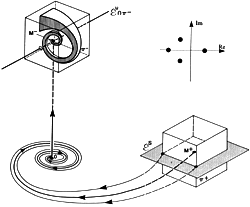
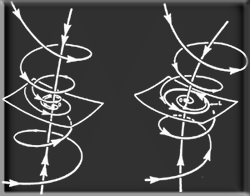
An introduction to discrete and continuous dynamical systems. Study of nonlinear dynamical systems, leading to chaotic behavior. Topics include: Phase space. Linear and nonlinear systems. Poincare maps. Structual stability. Topological conjugacy. Types of equilibrium states and fixed points. Periodic orbits. Stability. Local bifurcations. Homoclinic orbits. Routes to chaos. Applications from physics, biology, population dynamics, economics.

Prerequisites   MATH 3260 and 3435

Text  L.Shilnikov, A.Shilnikov, D.Turaev, and L.Chua, Qualitative Methods for Nonlinear Dynamics, Parts I and II, World Scientific Publ.

Topics   Basic concepts and definitions. Qualitative integration. Linear autonomous systems. Topological conjugacy. Periodic orbits. Poincare maps and fixed points. Floquet multipliers. Structural stability. Hyperbolicity. Bifurcations of equilibrium states and periodic orbits. Invariant tori. Bifurcations of homoclinic orbits. Smale horseshoe. Routes to chaos and strange attractors. Applications.

Course requirements Regular homework, 2 tests, and a final exam, which may be replaced by a project.

Justification   The idea that many simple nonlinear deterministic systems can behave in an apparently unpredictable and chaotic manner was first noticed by the great French mathematician Henri Poincare. Other early pioneering work in the field of chaotic dynamics were found in the mathematical literature by such luminaries as Birkhoff, Cartwright, Littlewood, Smale, Pontryagin, Andronov and his students, among others. In spite of this, the importance of chaos was not fully appreciated until the widespread availability of digital computers for numerical simulations and the demonstration of chaos in various real time systems. This realization has broad implications for many fields of science, and it is only within the past two decades that the field has undergone explosive growth. It is found that the ideas of chaos have been very fruitful in such diverse disciplines as biology, economics, chemistry, engineering, fluid mechanics, and physics.
The field of nonlinear dynamics is very active. Furthermore, there are numerous applications in the physical and biological sciences, economics, etc. There are graduate programs in nonlinear dynamics, and there is an abundance of problems arising from recent subfields, such as the control of chaos. Courses in the nonlinear sciences would add to both our undergraduate and graduate programs due to both its timeliness and interesting applications.
Many fascinating phenomena, such as our weather system for example, are intrinsically nonlinear. This course will provide an introduction to nonlinear behavior, principally through the study of differential and difference equations (maps). We will begin with a study of the stability of equilibrium states, fixed points and periodic orbits of one- and two-dimensional maps. This can be followed by the study of their bifurcations, and the analysis of saddle trajectories. This will lead us to emergence of strange attractors of fractal dimensions; the evolution of saddle orbits into chaos. It will lead to the idea that seemingly random behavior can emerge from perfectly deterministic systems. Many of the key ideas can be illustrated by fairly simple sets of equations that on a computer can be solved rapidly and accurately.
Nonlinear dynamical systems are used as models in every field of science and engineering. Universal patters of behavior, including chaos, have been observed in large sets of examples. Mathematical theories describing geometrically the qualitative behavior of "generic" systems explain many of these patterns. This course will discuss dynamical system theory and its application. Several representative examples from different disciplines will be described at the beginning of the course and used throughout the semester to illustrate theoretical ideas. Emphasis will be placed upon bifurcations, the qualitative changes in solutions of differential and difference equations that occur as system parameters are varied. Computational methods for the analysis of dynamical systems will be also discussed. Examples come from population dynamics (Voltera-Lotka model, period doubling cascade), physics (van der Pol and Duffing equations) meteorology (Lorenz model), chemistry (Belousov reaction), finance (low-order stock models, chaos); and normal forms from mathematics